
|
primenumbers web pageTweet |
|
Perspective |
|
We have the real system coordinates |
| We can transform from the real to the screen coordinates via the formulas: |
|
|
Triangle decomposition |
|
The extremes of the triangle chord have equations:
A point of the chord has equation :
So ,developing the calculus:
These are the barycentric coordinates of the point in the triangle:
|
Edge walking |
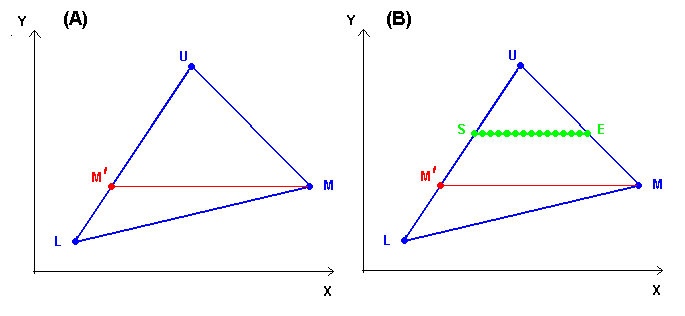 |
(A) Divide the triangle into 2 triangles with a common side parallel to the X axis.
(B) For each triangle locate on the edges wich are not in common a start point (S) and an end point (E) with the same Y coordinate.Then you can easily manage every pixel from S to E. |
Axonometric projection |
I use an oblique projection,where the projection plane |
The real point  is mapped in the projection point
is mapped in the projection point 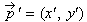 via the formulas: via the formulas:
|
|
Where |
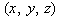 with
the observer placed in the points
with
the observer placed in the points 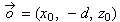 .The projection screen plane
is placed in
.The projection screen plane
is placed in 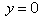 and the screen coordinates are
and the screen coordinates are 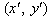 .
We have for simplicity the coincidence within the axis
.
We have for simplicity the coincidence within the axis 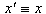 and
and
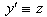
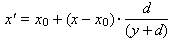
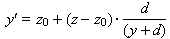
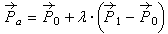 and
and
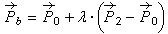 with
with
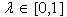
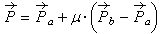 with
with
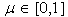 .
.
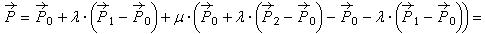

 with
with

 for simplicity coincide with
the real plane
for simplicity coincide with
the real plane 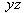 ,
with
,
with  and
and  .
.

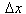 and
and  are the measure unit on the projection axes
, and
are the measure unit on the projection axes
, and 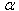 is the angle between the projection of
the x and z axes,and
is the angle between the projection of
the x and z axes,and 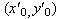 are the coordinate of the projection
of the real origin O.
are the coordinate of the projection
of the real origin O.